Calculus: Approaching Zero

I have to write this blog now, else it may take a long time to return to this topic. This journey of Maths (the language of universe) is so mind-boggling that one can easily get absorbed for an indefinite period.

I have read calculus many times. I know the formulae of differentiation. I don’t think there is any calculus student who doesn’t know y=f(x)=x². And the proof

But the puzzle of approaching Zero never leaves. I have watched hundredes of videos to understand the approaching Zero or infinitesimal small difference. This bloody thing drills a hole in your head leaving you with the feeling of ‘I will never understnad this in my life‘. Student is able to solve all the exam questions just the way a pilot is able to fly the plane without fully understanding the Bernoulli equation and he does absolutely fantastic in his professional life. But but that hole remains.

If you are not one of those students, then your journey ends here. You are the bright mind who cracked it. For less fortunate like me, lets continue. 🙂

Calculus works and works like a charm. Single variable, multi-variable, maxima, minima, local maxima, global minima etc etc. But this bloody close to zero …. hmmmm…

So, lets look into it. Once again.

Think of it; what are we trying to achieve? The answer is – Velocity of an object in motion at any given moment. Note- you take the scenario according to your field of expertise like thermodynamics or fluid mechanics or mechanical engineering or IT domain in motion (telecom, finance) etc. And what will you achieve if you identify that? The Rate of Change. It is this property that every dynamic system goes through. IT people- you think DATA. Am I trying to connect calculus to data? Yes Sir. The path will take you straight to the land of Artificial Intelligence (AI). How about Change itself? Its not the topic today. Its like looking into f(x)=x² and not its derivation. Another pandora box.

So back to the topic. This is the graph of y = x² looks like along with the slope or tangent or the rate of change at a given point.

The tangent at coordinates 1, 3 represent the rate of change and we achieved it using the derivation 2x meaning slope is positive 2. How? By going very close to that point. Almost zero but not zero. Come on man that’s what you promised to explain. Yes. Take a deep breath and think why it should work.

The magic is hidden in

OR

(x + h)² = x² + h² + 2xh

This is a very powerful concept. More that what you may have imagined. Look once again at how it plays out.

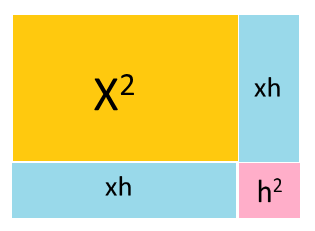
During the proof, despite cancelling x² and cancelling a major portion of h² , a considerable amount of area is still available to play around. As big as 2x + h. Mathematicians conciously decided to get rid of h (as it was quite small as compared to 2x).

It is this residue, a considerable residual distance, that gives us the slope at that moment. Not only that but it also helps to keep moving along with the path of the object. It produces such a powerful notion of movement that you feel as if you are moving along with the moving object. Now you not only have the velocity but also built the ground to calculate acceleration. The second degree derivative.

Now think of (a + b)3 = a3 + 3a2b + 3ab2 + b3 or differential of trignometry equations and you will realize even with approaching zero there is comfortable amount of playground.